The Pathfinder algorithm: the original, binary, Fast and MST-variants
The algorithm
A
Pathfinder
Network (or PFNET)
is a scaled network (or graph, in the sense of the graph theory) in
which weighted edges have been pruned in a specific way. Only those
edges which
do not violate the triangle inequality are kept. The triangle
inequality states that the direct distance between a couple of nodes
must be lesser than or equal to the distance between any other path
linking these nodes. The corresponding algorithm, first devised by
Schvaneveldt (1990) has two parameters: r,
which define the Minkowski r-metric used to compute the mentioned
distance, and q,
which define the maximum length of the paths considered in the triangle
inequality. Pathfinder Networks
are very important in the field of
social networks, in which it helps to exhibit a unique representation
of the underlying structure of the domain. In this context, the weight
of the edges often represents the similarity between the entities given
by the nodes.
According
to the litterature, the most used values for its parameters are r=∞, meaning that we keep the
edges having a value higher that the maximum similarity given by all
the other paths, and q=n-1,
meaning that we consider the paths having any kind of lengths,
including the maximal one, n-1.
MST-Pathfinder, up to our
knowledge, is the fastest algorithm to obtain Pathfinder Networks
for r=∞
and q=n-1.
Applications
These networks are used in a large
variety of applications including:
- Co-citation analysis (Buzydlowski, 2002)
- Latent knowledge visualization (Chen et al., 2001)
- Scientific domain visualization (Chen, 1998a)
- Communication networks (Shope et al., 2004)
- Animated visualization models of toxins (Chen & Morris, 2003)
- Mental models (Kudikyala & Vaughn, 2005)
- Debugging multi-agent systems (Serrano, 2010)
- and more recently the co-firing of rules in fuzzy systems
(Alonso, 2012)
More
resources
Additional
information on the Pathfinder Networks
can be found on the corresponding Wikipedia webpage: http://en.wikipedia.org/wiki/Pathfinder_networks
The
following table shows a comparison
of the variants of the Pathfinder algorithm, along with their
performance in terms of time and memory, took from the paper [3]. We
also provide a link to the source code (written in C). All ZIP
files contain a Makefile to compile the code on Unix-like
platforms, but the code should compile also on Windows-like platforms. In the following table, n is the size of the graph (number of nodes).
Name of the
algorithm |
Application domain |
Implemented application domain for the C code |
Time complexity
(for q=n-1) |
Space
complexity |
Approach in
algorithm theory |
Underlying
algorithm |
Download C Code |
Academic paper |
| Original PF |
Any valid values for q and r,
(un-)directed graphs |
Any valid values for q, r=+∞ (max),
(un-)directed graphs |
O(q · n3) = O(n4) |
2 · q · n2 = 2 · n3 - 2 · n2 |
Dynamic programming |
Schvaneveldt |
download link |
 |
| Binary PF |
Any valid values for q and r,
(un-)directed graphs |
Any valid values for q, r=+∞ (max),
(un-)directed graphs |
O(log(q) · n3)
= O(n3 · log(n)) |
4 · n2 |
Dynamic programming |
Schvaneveldt |
download link |
|
| Fast PF |
q=2 or q=n-1,
any valid values for r, (un-)directed graphs |
q=2 or q=n-1,
r=1 (sum), r=-∞ (min) or r=+∞ (max),
undirected graphs |
O(n3) |
3 · n2 |
Dynamic programming |
Floyd-Warshall |
download link |
 |
MST-PF
(theoretical) |
q=n-1, r=∞,
undirected graphs |
q=n-1, r=+∞ (max),
undirected graphs |
O(n2 · log(n)) |
3 · n2+n |
Greedy approach |
Kruskal |
download link |
 |
MST-PF
(practical) |
q=n-1, r=∞,
undirected graphs |
q=n-1, r=+∞ (max),
undirected graphs |
O(n3) |
3 · n2+n |
Greedy approach |
Kruskal |
download link |
 |
Important notices:
- The source code given above for MST-theoretical and MST-practical are exactly the same. You will have to change the value of the define called 'BASIC_FUNCTIONS' in the file global.h to select the desired behavior. With a value of 0 (the default option), we run the fastest version
of the algorithm which use index-based disjoint sets to store
intermediate results. Even if the theoretical time complexity is
larger, it is the fastest version: see the academic paper for more details. With a value of 1, we run the slowest version of the algorithm, which use the forest-based disjoint sets having the smallest time complexity.
- In all the variants above, and because we have implemented it for a specific case, which is the study of the Visual Science Maps, or Scientograms, the weights of the edges of the graphs correspond to a similarity
and not a distance (we are looking for a network having larger
distance or weight values for their edges, so we are pruning the edges
having small values).
- For the same reason, we have only implemented the case r=+∞ for
the Original, the Binary and the MST variants of Pathfinder, even if
theoretically (and easily), other values of r can be used. r=+∞,
which consider that the weight of a path is equal to the maximum
value of the weights of any of its edge, is also the most common
scenario. This allowed us to directly hard code the computation of the
maximum instead of the Minkowski metric which would have been slower.
Please, check the functions Programacion_Dinamica() or sumasims() if you need to change this behavior. For the Fast variant of Pathfinder, we have implemented three possible values for r (1, -∞ and +∞): other values for the Minkowski distance parameter can be easily implemented (check andupdate_weight_maximum() update_weight_minimum()).
- It is not possible to use any values for q
with Fast Pathfinder or MST Pathfinder, without substantial changes,
because of the underlying algorithm. With Fast Pathfinder, it is
however possible to use any r.
We show here the CPU computation time in seconds (on a Intel
dual-core Pentium 3.2 GHz with 2 GB of memory) for several random
generated graphs, to show the improvements obtained between these
different variants:
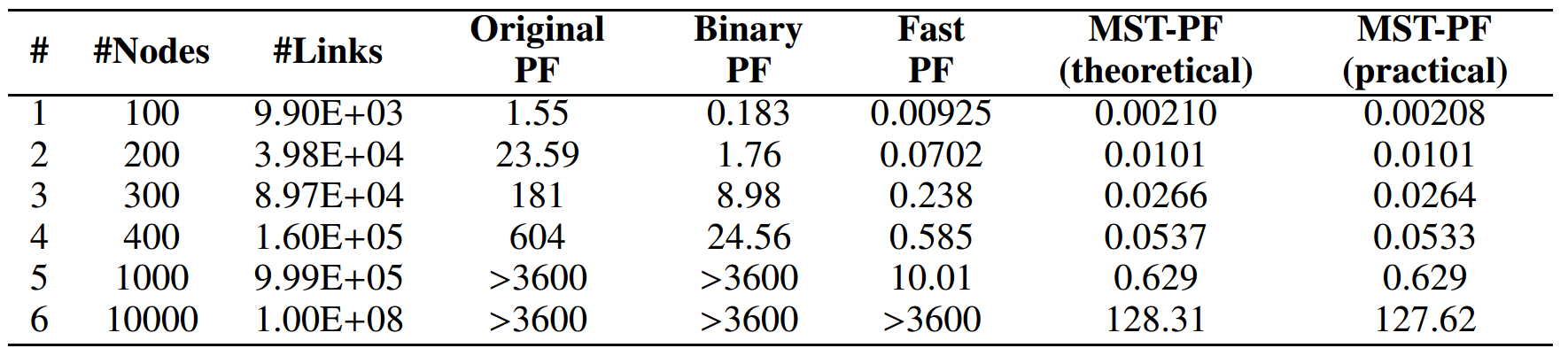
Example of a data file
Example of a graph given in the format of Pajek, by edges. In the
"vertices" section, the nodes are given by an index and a description.
In the "edges" section, the edges are given by the starting node (first
node = 1), the ending node, and the weigth of the edges (it can be a
real value, but cannot be negative). Edges do not need to be sorted in
any way. Edges which does not exist are simply omitted.
 |
Description in Pajek format:
*vertices 5
1 "1"
2 "2"
3 "3"
4 "4"
5 "5"
*edges
1 2 1
1 3 4
1 4 2
1 5 2
2 3 2
2 4 3
3 4 3
3 5 1
4 5 3
|
|
Example of the same graph given in the format of Pajek, by an adjacency
matrix. In this case, in the "matrix" section, we directly have the
weights for each edges (it can be a real value, but cannot be
negative). If you use r=∞ (max) you can encode a non existing edge by using a very small value (0). If you use r=-∞ (min), use a very large value. For undirected graphs, the matrix has to be symmetric.
 |
Description in Pajek format:
*vertices 5
1 "1"
2 "2"
3 "3"
4 "4"
5 "5"
*matrix
0 1 4 2 2
1 0 2 3 0
4 2 0 3 1
2 3 3 0 3
2 0 1 3 0
|
|
After the application of Pathfinder, the output obtained is:
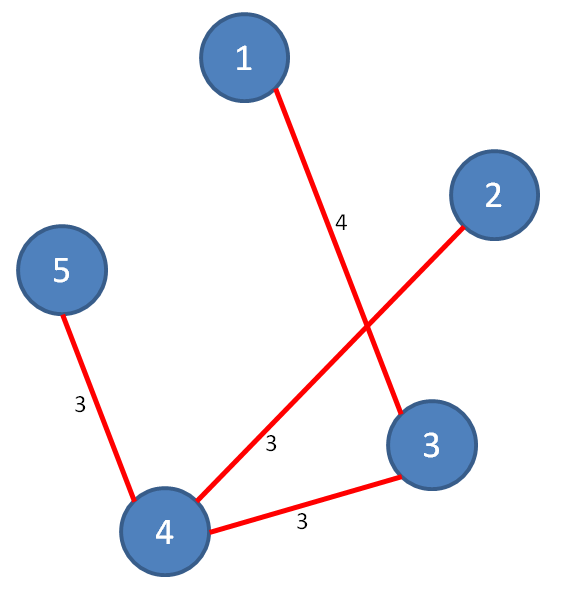 |
Description in Pajek format:
*vertices 5
1 "1"
2 "2"
3 "3"
4 "4"
5 "5"
*edges
1 3 4.000000
2 4 3.000000
3 4 3.000000
4 5 3.000000
|
|
More (small) example maps are given here: download link
Running the source code
After the compilation (just type 'make' in command line on Linux), run it this way, depending on the algorithm:
Original PF: <program> <filename> [<q>]
Binary PF: <program> <filename> [<q>]
Fast PF: <program> <filename> [q [r [direction]]]
MST-PF (all versions): <program> <filename>
-
<filename> indicates the filename of the Pajek-formated description of the graph. Both 'edges' and 'matrix' formats are supported. Only matter the edge
weights, not the node weights or descriptions (this one is used by
Pajek to print the graphs). Check the description of the format here.
- <q> defines
the maximum length of the paths considered in the triangle
inequality. If not specified, q=n-1 is ued.
- <r> defines the Minkowski distance parameter: 1 means the sum, 0 means infinity and could mean the minimum or the maximum (see direction).
- <direction> :
if 1, we compute the maximum paths (we keep edges with the highest
values). If 0, we compute the minimum paths (like in the original
Pathfinder in the book ofSchvaneveldt).
In case of errors.... here is the checklist
If MST-Pathfinder gives a segmentation fault, please
check your input file. The following checks have not been implemented
to provide the fastest possible implementation for correct files, but
any non valid file cannot be processed:
- The number of nodes N in the first line should corresponds to the actual number of nodes encoded in the following lines.
- In the 'edge' section, the node indices have to be between 1 and N, inclusive.
- Edge weights have to be positive or null. Because MST-Pathfinder
considers only the maximum of the weights, it should be always possible
to shift your set of values to a positive set by adding some constant.
- The matrix weights has to be symmetric. W[i][j] == W[j][i]. If it
is not the case, some values will be ignored. It is possible however to
define only the upper or lower triangle, that is encoding W[i][j] but
not W[j][i]. In this case, MST-Pathfinder will copy the value in the
other triangle.
- Weights on the diagonal have to be 0.
- No large values. The current implementation use the type 'double'
so the maximum value is around +/-2.2 e +/-308. Any superior or
inferior values may not be read properly.
Other known implementations
Relevant
publications
[1] R. W. Schvaneveldt
(Ed.); Pathfinder
Associative Networks: Studies in Knowledge Organization; Norwood, NJ:
Ablex (1990).

RECEIVED:
16/4/2007; REVI
[2] A.
Quirin, O. Cordon, J.
Santamaria, B. Vargas-Quesada, F. Moya-Anegon; A new Variant of the
Pathfinder Algorithm to Generate Large Visual Science Maps in Cubic
Time; Information, Processing & Management Journal, 44(4):
1611-1623
(2008).

RECEIVED:
16/4/2007; REVISED:
3/9/2007; ACCEPTED:
8/9/2007;
IMPACT
FACTOR
2007: 1.500.; CATEGORY: COMP.
SCI., INF. SYST; ORDER:
27/92; DOI:10.1016/j.ipm.2007.09.005
[3] A.
Quirin, O. Cordon, V.
P. Guerrero-Bote, B. Vargas-Quesada, F. Moya-Anegon; A Quick
MST-based Algorithm to Obtain Pathfinder Networks; Journal of the
American Society for Information Science and
Technology, 59(12): 1912-1924 (2008). 
SUBMITTED:
12/9/2007; REVISED:
21/2/2008; NOTIFICATION
OF
ACCEPTANCE: 14/4/2008; PUBLISHED: 8/7/2008; IMPACT FACTOR 2007:
1.436;
CATEGORY: COMP. SCI., INF. SYST; ORDER: 29/92; DOI:10.1002/asi.20904
[4] E.
Serrano, A. Quirin, J. Botia, O. Cordon; Debugging Complex Software
Systems by Means of Pathfinder Networks; Information Sciences, 180(5):
561-583 (2010).

NOTIFICATION
OF
ACCEPTANCE: 3/11/2009; IMPACT
FACTOR 2009: 3.291; DOI: 10.1016/j.ins.2009.11.007
Last updated: 10/11/2014. A special thank
to Oscar Cordon and David Pérez Pancho for their corrections and
suggestions about the source codes and the algorithms.


